タイトル：「フロントローディングおいて良い案をマイニングする」

サブタイトル：「意思決定の高度化」「BIM時代に数の海で溺れないために」「設計者による簡単な統計」

0：Part 01の振り返り

この投稿はPart 01の続きです。
Part 01ではこの投稿の意図・問いと場面を共有させて頂きました。

短めにでもPart 01をご覧になって頂きたいのですが簡潔に示すと，
投稿の意図は，

「定量的な計画手法」という言葉が，BIM時代の到来により，BIMと古典的な（＝中身が分かり共有できる）統計を併せることで誰もが意思決定の場で使える「道具」になっていることを共有したい

です。

問いは，

「BIM」を使えばフロントローディングで「早期に質の高い意思決定」を行うことができるのでしょうか？

「企画チーム，偉い人，信用できそうなベテラン，先導的で扇動的な建築家，科学的な背景がありそうな専門家，高度で難解な説明をする有識者，そして施主，これらでワイワイガヤガヤと集う意思決定と称した長い会議をBIMにより進歩させるイメージはありますか？」

です。（二つ目は失礼ながら敢えて挑発的に言い換えた問いです）

場面は「多面的な可能性に対する多様な評価がBIMによって出揃った段階の意思決定」です。
極端に例示すれば100案に対する100種の評価（大量の報告書？）が揃った後，という場面です。

それでは振り返りはこの程度とし，Part 02の内容に移りたいと思います。
長いですがお付き合いください。

３：良いコンセンプトモデルをマイニングする

ここからがこの投稿の本題です。少しばかり統計を用いますが，意外と使えるぞ統計，しかも簡単だね，と思って貰えれば嬉しいです。

紹介する統計手法はと「標準化」と「外れ値」です。

「。。。。。は？」と思った方が大多数でしょうか？
そう，大学の卒業論文どころか，最近では高校で学習するような内容です。しかし侮ってはいけません。
高度で厳密であることは重要です。しかし高度で厳密（その代わり難解）な手法であればいい訳ではないのです。
簡単であることも重要です。簡単であるということは「簡単である＝中身が分かる＝具体的に共有できる＝人が介在できる」ということです。
そう，卒業設計で卒業した人でも（自分もそうです）。
この投稿では企画チームの統計担当以外のメンバーにも具体的に共有できる，ということも優先してこれから手法を紹介します。
それでは，ここからは仮想の数字を使いながら，「外れ値」「標準化」という簡単かつ古典が意外と？使えることを紹介します。

3.1:　例示の状況確認

ここからは例示として仮想の数字を扱います。そこでまず例示の共有をしたいと思います。
案は100案（サンプルとも称します）です。
次に評価です。以降，評価に使った指標は変数・評価変数とも称します。なお評価変数は例示ですので，かなり減らして8変数とします。
評価変数の項目にはまずシミュレーションを採用します。この投稿では具体的な項目が何であるかは問題ではありませので，イメージしやすいように環境・構造・設備・施工・管理・価格，と項目だけ命名して終わります。
次に，評価変数にデザイン性が含まれないのは残念ですので，SD法を用いたアンケート結果も採用します。エンジニアの方には馴染みがないかもしれませんが，「ランドマーク性」「美観性」などを５段階程度の尺度で測るものです。これを企画チームグループ（自己評価）と複数人の他者グループ（他者評価）で実施したとします。

注釈：「SD法を比例尺度とみなすか？」については古来から議論が続いているのですが，今回は量的に扱い，正規性も確認された，という前提とします。同じくシミュレーションも安易に複数回の平均値を結果の代表値として採用することは望ましくないのですが，今回は代表性のある平均値が形成されたとして平均値を採用します。

これでパラメタリックに生成した100案を評価する８変数（Variable）が下記のように揃いました。
10案までを表示した表になっていますが，例示の状況をイメージしやすいようにという意図で表形式にしているだけで，それ以上の意味はありません。

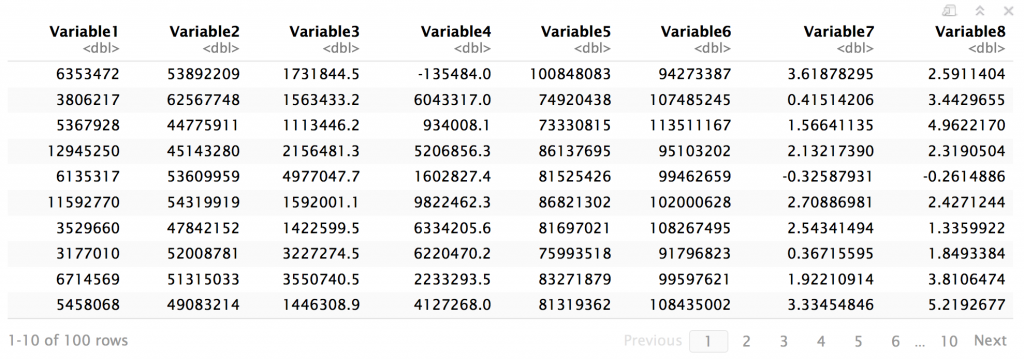
さて，仮想の数字でなくても，意味の分からない，つまり解釈がしづらい状況です。
ここから結果（大量の報告書）をまとめて解釈してコンセプト案を選定する一例を段階的に紹介します。

最初の留意点

コンセンプトモデルの選定する，とはデータをまとめて解釈する，ということです。
しかし例示のケースではまとめて解釈する際に「単位と値の範囲が異なる」ということが最初の留意点になります。
至極当然のことですが，８変数をまとめて解釈するには最初にこれが障害となります。
1案対する8変数を代表する値が欲しいけれどそのまま四則演算できない状況です。
価格であれば単位は円です。SD法であれば単位は無次元。価格の最大値は億にもなりますが，SD法は最大で5です。
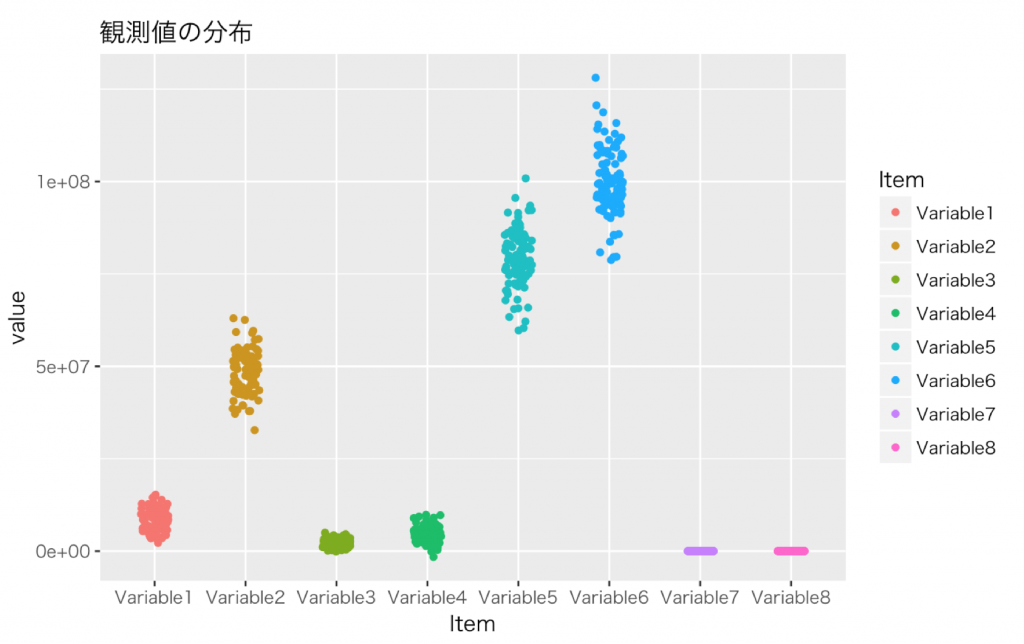
単位を無視する暴挙に出て無理やり図にすれば下のようになります。（X軸が変数，Y軸が観測値）
当然，このような状況のままで合算した場合にはSD法の意味はほぼ0になります。

3.2:　「標準化・標準得点」

このような時に用いるのが「標準化・標準得点」です。（Z得点化，Z得点とも呼びます）
馴染みが薄い用語かもしれませんが，ほぼ全ての人に馴染みのある「偏差値」の元となる数字です。
標準得点はこの投稿の意図である案が優れているかを定量的には判断する，といった際に使いやすい値の変換です。
そのため変数毎にプロット図を作ったり，最小を0・最大を1とする正規化ではなく標準化を紹介します。
なお標準化により分布の形状は変わりません。

それでは「標準化」します。
標準化の説明を後述しますが一旦読み飛ばしても大きな差し支えありません。

＊＊＊ここから＊＊＊
「標準化」とは観測値の「偏差」を「標準偏差」で除して「標準得点」に変換することです。
「偏差」は各値と平均値の差，平均からの偏りの度合いです。
「標準偏差」はある評価変数内での値の散らばりの度合いを示し，大きいほど散らばりが大きく高い値も小さい値もある，という状況を表現しています。
「標準偏差」は「分散」の平方根です。
「分散」は「偏差平方和」を「サンプル数」で除した値です・
「サンプル数」は今回の場合だと案の数が該当します。
「偏差平方和」は「偏差」を平方（二乗）して足し合わせた値です。
つまり，各値が平均から離れたいる度合いを大きさにして（二乗して）足し合わせ，サンプル一つ当たりの大きさにしたものが「分散」です。
ただこのままだと単位が観測単位の二乗（例えば円の二乗）で意味が解釈しづらいので，平方根をとって単位を観測単位に戻したものが「標準偏差」です。

なお厳密には，「サンプル数」で「偏差平方和」を除した値を「（標本の）分散」，「サンプル数−１」で除した値を「不偏分散」と呼びます。
そして，「（標本の）分散」の平方根を「標本（の）標準偏差」，「不偏分散」の平方根を「標準偏差」と呼称します。
呼び方は様々あるのですが，少なくともこの投稿ではこのように呼称します。
なお使い分けとしては，推測統計の文脈では「不偏分散」から算出した「標準偏差」を用いますが，記述統計の文脈では「標本（の）標準偏差」を使います。実は今回の場合だとどちらを使うのが適切か難しいのですが，話がこれ以上長くなってはいけないので「標準偏差」を使います。
（ちなみに難しいのはそもそも母集団を仮定するのか，という問題に対する解釈です）
＊＊＊ここまで＊＊＊

標準化によりできることは，あるサンプルの評価値が平均から標準偏差で何個分偏っているか（優れているか，劣っているか）という解釈です。

，，，イメージしづらいでしょうか？
イメージしやすいように「偏差値」を例に紹介します。
「偏差値」は「標準得点」を10倍して50足した値です。つまり標準得点2と偏差値70は同じ意味を持ちます。
理論的な背景を知ることが大切なのですが，偏差値60と言ったらまぁまぁ高い，偏差値70といったら結構高い，偏差値80といったらあり得ないほど高い，と感覚的に分かりますね。実はこの有り得ないほど高い，というのは理論的な背景にマッチングした感覚なのですが，今回は紹介を控えます。
実務上はこのような感覚的な理解を持つだけでも有用と思います。
理論的な背景を知るには「正規分布・確率分布・確率密度関数・サンプリング分布・中心極限定理」などを調べてみてください。

標準化の要点をまとめと，

標準化すると，観測時の単位と範囲にかかわらず，単位は「標準偏差」，平均は「０」（分散は１）となる。
これにより，異なる評価変数でも標準得点２であれば，観測単位が円でも日射取得量でも平均値からの偏りの程度という同じ意味となる。
結果，あるサンプルの評価値が平均から標準偏差で何個分偏っているか（優れているか，劣っているか），という解釈が可能になる！

ということです。

下図は標準化した結果の標準得点（Z得点）の分布です。（X軸が変数，Y軸がZ得点）
(どれも綺麗すぎるほどの正規分布状で不自然ですが，正規分布を仮定した乱数から例示を作成しているためです)

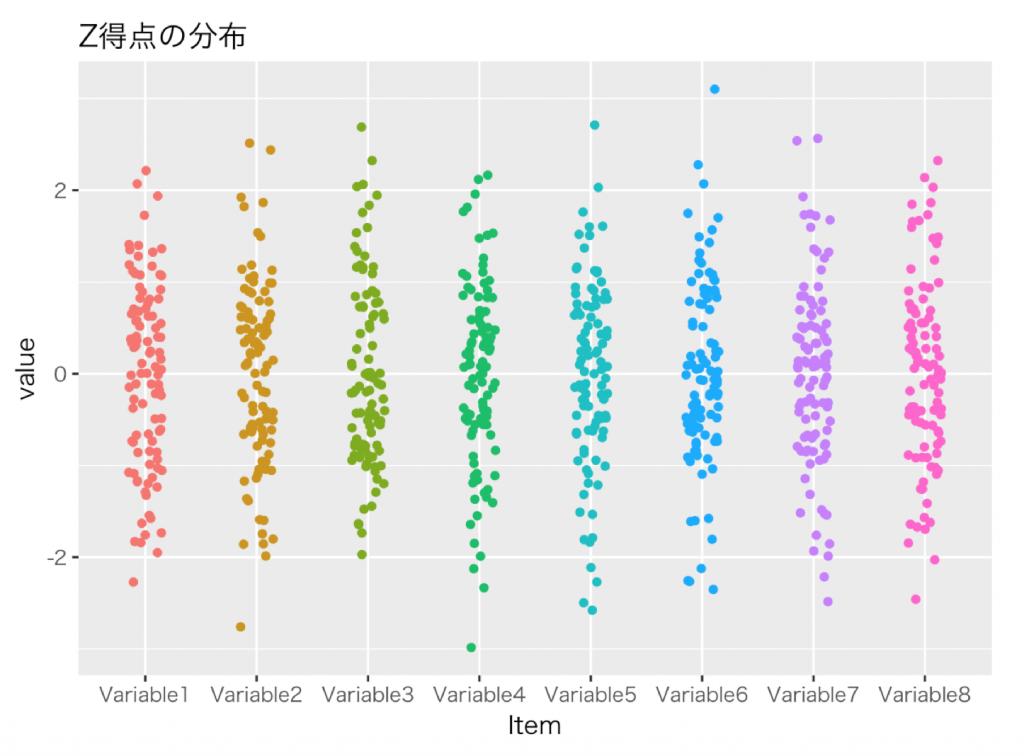
これで億になる価格が，SD法を用いた最大でも5の意味は消し去ることは無くなりました。
また各値が平均的な案からどの程度優れているか・劣っているかの程度を示す値になりました。
この程度が総合的に優れていれば相対的に良い案ですので，合算します。

注釈：もしこの段階でデザインを重視したい！，環境をコンセプトにしたい！という企画チームの意思がある場合はその評価変数の標準得点を任意倍する（重みを付ける）こと等も可能です。

合算した標準得点の分布が下図です。（X軸が各変数のZ得点の合計，Y軸の値に意味なし）

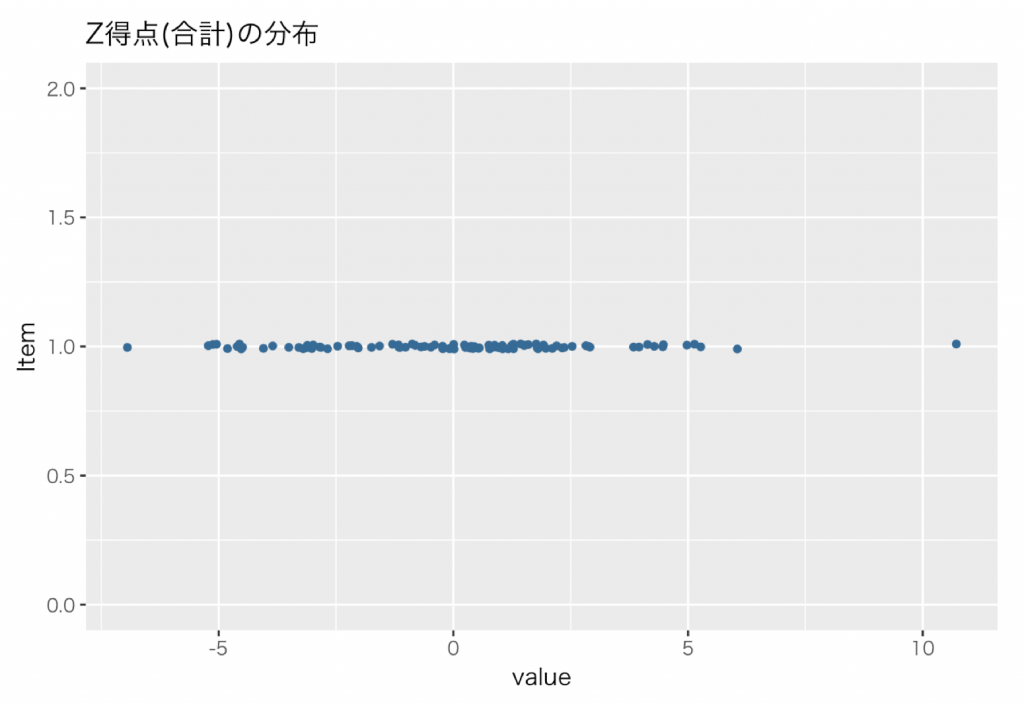
ようやくこれで8種の評価変数が一つの総合得点という合成変数になり，100案に対して100個の点数という状況になりました。
では，一番高い案を採用しましょう！
下記が高い順に並べた表です。（IDがサンプルの識別番号，valueが各変数のZ得点の合計，Rnakが順位）

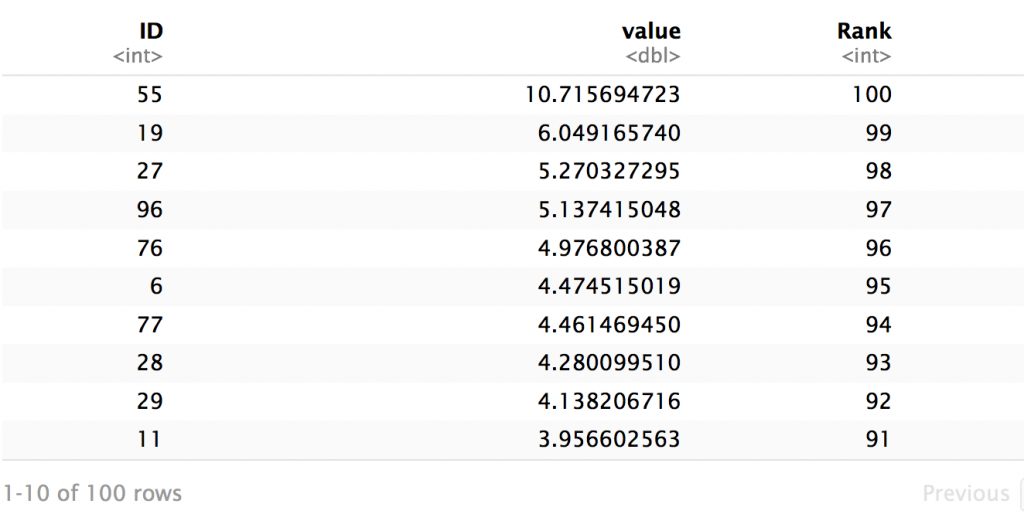
1番高い案の得点は約10.71です。２番目に高い値は約6.04です。3番目に高い値は5.27です。以下，続きます。
値が示す意味は前述の説明とほぼ同じように解釈して大きな差し支えはありません。各サンプルの８変数の平均からの偏りの程度です。
１番目は比較的突出して高い気がします，しかし２番目と３番目は比較的近い値で，，，，と続きます。
そのため，最後に，全体の分布に案の得点を位置付けた上で，大きいか小さいかを判断する必要があります。
これが本投稿の最後の工程です。

注釈：主成分分析という選択肢（一旦読み飛ばして後で読んで頂いても大きな差し支えはありません）
少し余談と言いますか，留意点です。
上記のように異なる変数の合成変数を作って評価したい場合，頻繁に用いられる手法は「主成分分析」です。
主成分分析とは，合成変数として各サンプルの情報量が多い主成分（軸）を分析する手法です。
情報量を最大化する，という観点から分散が最大となる主成分（軸）を抽出する，という手続きにより分析します。
2変数で言えば，2軸の散布図のプロットに対して直線を引く時に，直線に向かって垂直に下ろした各値の値の分散が最大になるように直線を引く，ということです。
多変量（複数の変数）に対して用いることが多く，共分散行列・相関行列の分散が最大となる主成分（軸）を分析します。つまり対象となる行列の固有値・固有ベクトルです。
こちらの方が良い気もしたのですが，情報量の最大化＝分散の最大化であること，それが固有ベクトルであることは分かりづらいかもしれません。
この投稿では，厳密であることよりも，簡単で企画チームの統計担当だけでなく全員が具体的に理解して議論が可能であることも重要視しています。
これを優先して標準得点を足し合わせる，という方法を紹介しています。このため，合成変数形成における各変数の重みの把握，相関関係は興味の対象外とあり，合成変数が１変数で形成されることを前提としています。
これをふまえると，統計担当が主成分の形成を確認した上で，会議資料としては標準得点の合計を用いるという運用が適切かもしれない点が留意点です。
さらに余談ですが，主成分にすればいいと言う訳ではありません。X割程度の分散説明力で主成分とみなす，というXには分析者の論理的な判断（若しくは分野のお作法）が用いられますが，必ず情報が欠損していることにも注意する必要があります。

注釈：異なる変数の標準得点の四則演算することの２つの主な留意点（一旦読み飛ばして後で読んで頂いても大きな差し支えはありません）
余談が多くなりますが，また留意点です。
・１つ目
重要な留意点は，合計点の偏差値と，偏差値の平均（合計）では，サンプル間の順位が入れ替わる場合がある，ということです。
実は上記のような異なる変数毎の標準得点を合計（平均）する，という手続きは一般的とは言えません。
同じ意味を持つ偏差値で考えれば，科目毎の偏差値を平均する（合計）する，と同じ手続きです。
受験の場合は合計点が合否判定において重視される傾向が強いので，このような総合判断を行いたい場合には合計点の偏差値という選択肢があり得ます。
それでも画一的・一般的に頻繁には用いられていないのは筆者の印象です。（総合判断における得点の扱いは予備校や大学毎で異なるようです）
これに倣い，今回の場合でも，合計点の標準得点を総合判断に使うという選択肢はあり得ますが，値の範囲が大きく異なります。
また今回のような標準得点の合算（平均）にはコンセプト案の変数毎の特性が反映されます。（A君は英語が突出して得意など）
この投稿の文脈ではこのような手続き上に含まれる性質は好ましいと考えて，異なる評価変数の標準得点を合算（平均）する，という手続きを紹介しています。
・２つ目
次の留意点は統計を用いた解釈に対する厳密さに関わる内容です。（厳密さは投稿の意図に反するので短めに記述します）
これは異なる分布が混ざってしまい，本来の標準得点の解釈に疑義が生じるかもしれない，ということです。
これは特には，後述する「スミルノフ・グラブス検定」の前提条件に関わる内容で，研究論文では見過ごせない内容です。
推測統計の基礎知識の説明が必要になり長くなりますので割愛しますが，厳密には手続きの適切さに疑義が生じる可能性がある，ということは留意してください。
今回は大変きれいな結果が得られていますが，これは正規分布から乱数を作っているためです。

準備が終わり，いよいよ意思決定ですが，Part 02はここまです。ぜひ次の投稿もご覧頂ければ幸いです。

Part 03へ