タイトル：「フロントローディングおいて良い案をマイニングする」

サブタイトル：「意思決定の高度化」「BIM時代に数の海で溺れないために」「設計者による簡単な統計」

0：Part 02までの振り返り

この投稿はPart 01，Part 02の続きです。

Part 01ではこの投稿の意図・問い・場面を共有させて頂きました。

まだの方はご覧になって頂きたいのですが，投稿意図は，

「定量的な計画手法」という言葉が，BIM時代の到来により，BIMと古典的な（＝中身が分かり共有できる）統計を併せることで誰もが意思決定の場で使える「道具」になっていることを共有したい

です。

問いは，

「BIM」を使えばフロントローディングで「早期に質の高い意思決定」を行うことができるのでしょうか？

「企画チーム，偉い人，信用できそうなベテラン，先導的な（扇動的な？）建築家，科学的な背景がありそうな専門家，高度で難解な説明をする有識者，そして施主，これらでワイワイガヤガヤと集う意思決定と称した長い会議をBIMにより進歩させるイメージはありますか？」

です。（二つ目は失礼ながら敢えて挑発的に言い換えた問いです）

場面は「多面的な可能性に対する多様な評価がBIMによって揃った結果が出揃った段階の意思決定」です。

次にPart 02についてです。

Part 02では，例示データを紹介し，案を選定（意思決定）するための準備として例示データを標準化しました。
例示データは，100案に対する８評価（変数，大量の報告書？）というデータ（行と列からなるマトリックス表）です。
この投稿の文脈において「案を選定する」とは，「データまとめて解釈して，値の大小を判断する」ということです。
そこでPart 02ではこの準備として標準化・標準得点という値の変換を紹介しました。
イメージしづらいと思いますのでぜひ短めにでもPart 02をご参照ください。

それでは振り返りはこの程度とし，Part 03の内容に移りたいと思います。
聞きなれない用語も出てきますが，お付き合いください。

3.3:　選定する

それでは，コンセプモデル候補を選定するために各案の得点の大小（案の優劣）を判断します。
各案の得点の大小の判断とは，得点を全体に位置付けて大きいか小さいかを判断する，ということです。
この投稿ではこの方法を「記述統計」と「推測統計」の文脈から二つ紹介します。
「記述統計」の文脈からは「外れ値」を検出する方法です。
「推測統計」の文脈からは再度「標準化」してその標準得点を解釈する方法です。（外れ値の検定に相当します）
最後に，これを組み合わせた図を紹介します。

3.3.1:　「外れ値」

では記述統計の文脈における「外れ値」の検出です。
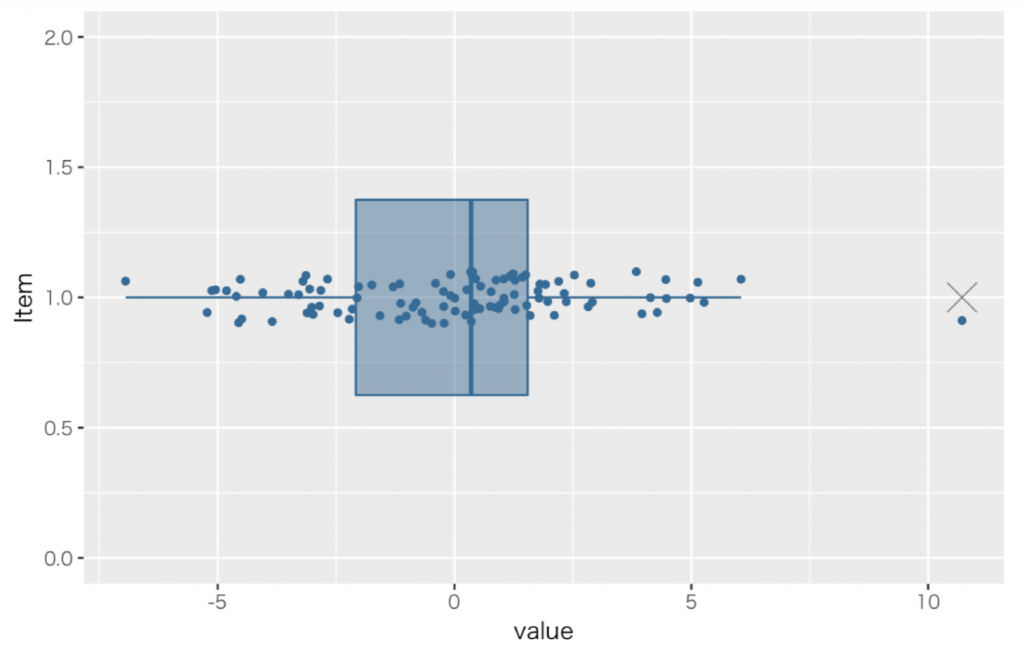
これを見るには箱ひげ図を描画するのが便利です。（X軸が各変数のZ得点の合計，Y軸の値に意味なし）
箱ひげ図はインターネットに情報が多く理解も容易ですので説明は省略します。

結果，一位の案（約10.71点）が外れ値となりました。この案は統計的に外れ値と言えるほど100案の平均的な評価よりZ得点が突出して高いと言えます。
一般的には，外れ値は同じグループに属すると判断して統計を進めるのが適切とは言えないサンプルを検出するのに用います。
しかし今回の文脈ではこの外れ値となったサンプルが重要です。
この投稿の文脈においては，外れ値と言えるほど突出して優れた案，つまりコンセプトモデル候補になる案と言えるでしょう。
なおの2位の案（約6.04）は順序としては２番目でしたが，ひげの中に収まる程度で，外れ値と言えるほど突出して優れた案と言えるほどでない，ということです。
（但しひげの長さはチームの判断で変えることもできます。）

3.3.2:　「スミルノフ・グラブス検定」

では次の方法です。次の方法は推測統計の文脈における「外れ値」の検定です。
こちらも外れ値に相当するのですが，呼称が同じだとややこしいのでこちちらを「スミルノフ・グラブス検定」と呼称します。
「スミルノフ・グラブス検定」という難しそうな用語が登場してしまいましたが，紹介する方法は検定そのものではないので安心してください。
ここまできて難しそうな用語で煙に巻くことをしません（笑）。統計に馴染みのある方はこの用語の方が内容を把握しやすいかも，と思い紹介したまでです。
ただ紹介する方法はとても簡単ですが「スミルノフ・グラブス検定」に相当する方法です。
行うことは「Z得点の合計点（平均点）をさらに標準化する」だけです。
下図がその結果です。（X軸が各変数のZ得点の合計のZ得点，Y軸の値に意味なし）

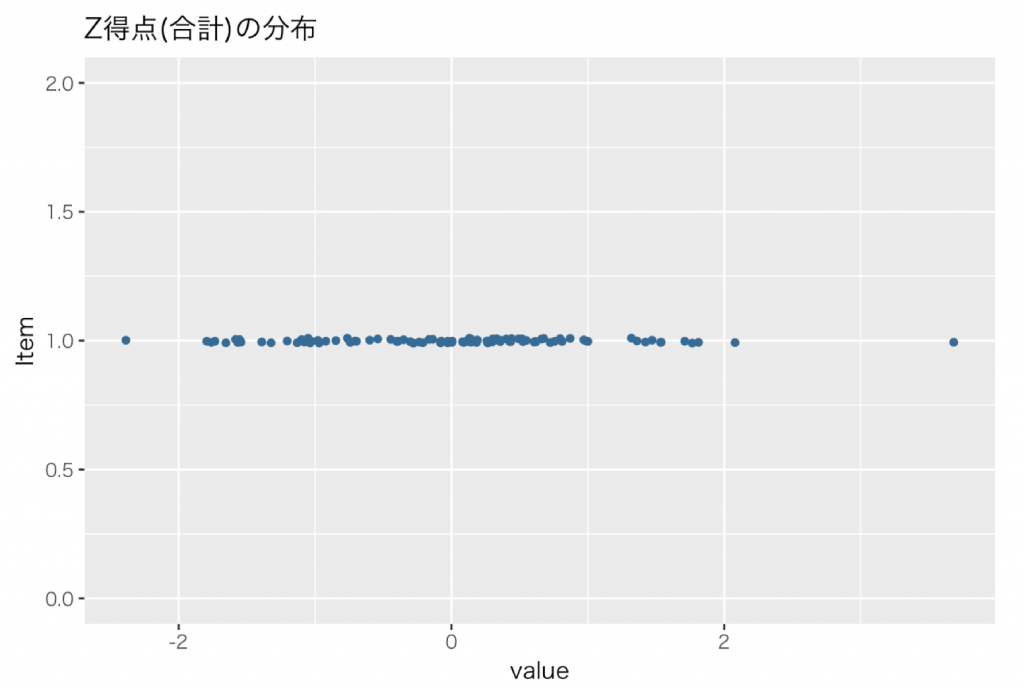
。。。おや？
上図と分布が同じです。またPart 02Z得点の合計の図とはの軸の数値が変わっただけで全く同じですね。何故なら上述したように標準化は分布の形状を変えないからです。
但し，解釈においては軸の数値が変わったことに重要な意味があります。
少し図を変えます。

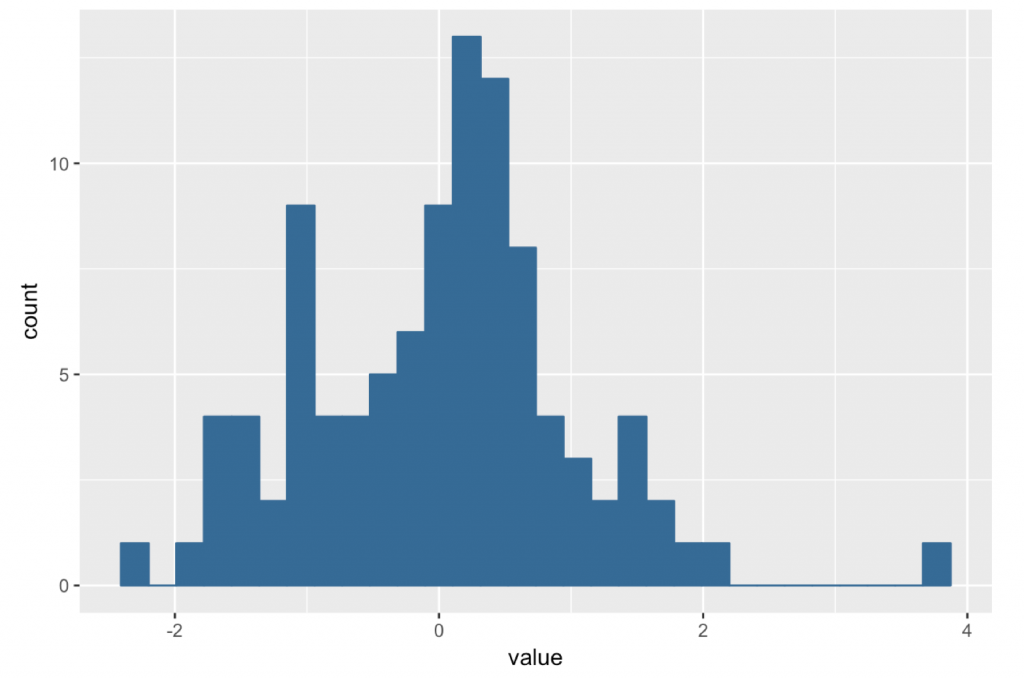
ヒストグラムにしました。（X軸がZ得点の区間，Y軸が度数）
この図は値の範囲を分割して各区間に何案が含まれるか，を示した図です。
今回は100案なのでそれなりに綺麗な正規分布，程度ですが，正規分布状の確率密度曲線に近似できると判断できる場合，「得点2」以上が観測される確率は約2.5%です。
言い換えると，無数に案を立案し，その評価のサンプリング分布が正規分布であると仮定した時に，「得点2」以上は上位2.5%になると期待されるほど突出して優れた案，ということです。つまりコンセプトモデル候補になる案と言えるでしょう。

注釈：統計を研究に用いる場合には「仮定が満たされるか」ということは決して無視できません。
ただ会議の前に案をクリーニングする，議論の土台・開始地点にする，という利用程度でしたら大きな差し支えは無いと思います。
また前述のようにこの方法は「スミルノフ・グラブス検定」に相当します。
検定の言い方に直すと「全てのサンプルが同じ母集団からサンプリングされたものであるとは言えない」「約10.71点の案は外れ値である」です。
手順の違いは，帰無分布（帰無仮説「全てのサンプルは同じ母集団からサンプリングされたものである（差がない）」を想定したサンプリング分布）に値を位置付けて確率を算出するかしないかです。
合計した場合の最高得点である約10.71点を標準化した3.6833は，検定を実施した場合の検定統計量に一致します。
なお検定を実施すると，p-value = 0.006906となり，5%水準において有意な結果となりました。
（「推測統計」「スミルノフ・グラブス検定」というと難解そうですが，簡単かも？，と統計に馴染みのない方に思って貰えると投稿意図とは関係ありませんが嬉しいです。）

3.3.3:　「両方を同時に視覚的に判断する」

最後に両者を同時にみる方法です。
これは単純にZ得点の合計を標準化した値の箱ひげ図を見れば一目瞭然です。（X軸が各変数のZ得点の合計のZ得点，Y軸の値に意味なし）
外れ値であり，かつ２以上である案はあるかな，ということが視覚的に直ぐに分かります。

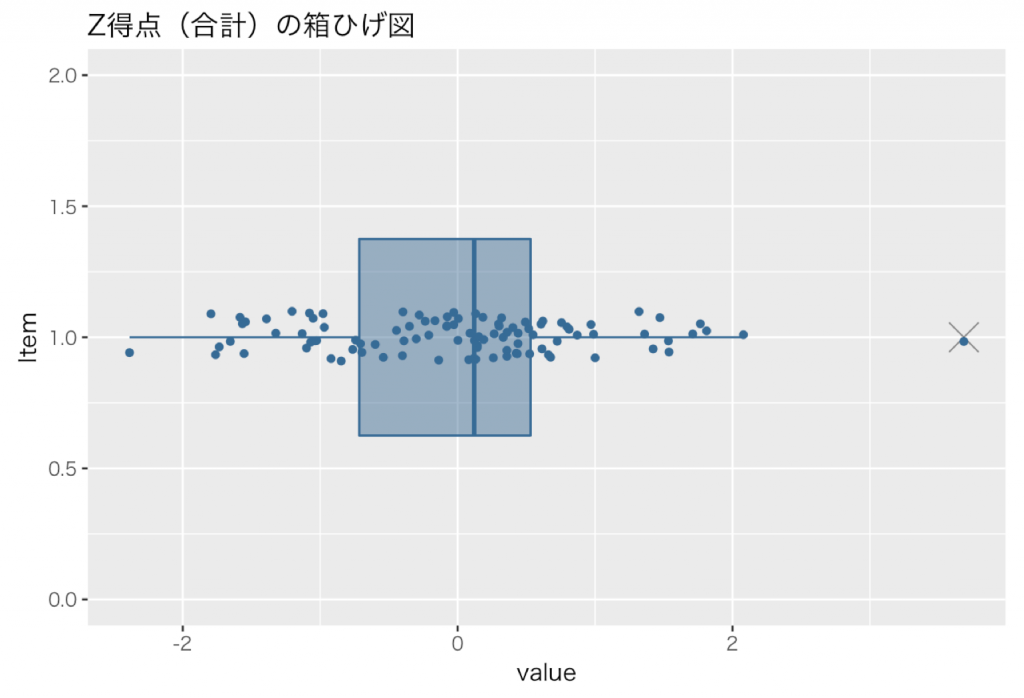
この図を見ると，
１番目に得点が高い案は，両方の観点から突出していると言及できるほど優れた案，と言えることが視覚的に直ぐにわかります。
また2番目に得点が高い案は，Z得点の合計のZ得点は２以上だけど，順位の観点からも外れ値と言及できるほど優れた案と言える程ではない，ということが分かります。
加えて3番目に得点が高い案は，Z得点の合計のZ得点は2以下で，順位の観点からも外れ値と言及できるほど優れた案と言える訳ではない，ということが分かります。

なお「スミルノフ・グラブス検定」の文脈において，得点1.5と1.4の差，2.1と2.2の差のもつ確率的な意味は違います。
また，2以上であるということは絶対的な基準ではありません。慣習として頻繁に用いられる目安はありますが，分野によって異なります。
なお今回の文脈であれば，企画チームが上位何％を優れた案と考えるかによって値を決めることも可能です。

以上です。

注釈：一連の投稿ではいくつかの厳密さを保留していることに留意してください。
大変きれいな結果が得られましたが，これは正規分布から意図的に乱数を作っているためです。

4:　終わりに

このような資料が人同士の意見交換より優れているとまでは言えません。
また結果に対する議論を経ずに統計結果をそのまま採用するのも不適切です。
統計がある程度分かるメンバーがいない状況でこのような資料を単に機械的に作って使用するのもあまり適切ではないでしょう。
しかしこのような資料から議論を始めることは，「フロンローディングにおける意思決定」を高度化する上で役に立つのでは？，と考えています。
なお投稿は説明が冗長で長くなりましたが，実行はあっという間です。そのため少し飛躍しますが，パラメタリックデザインとシミュレーションの一連の流れをプログラム化すれば，案を一種のビックデータ（作成者の意図を超えた部分も含む大量のデータ群）ととらえて案をマイニングすることも出来るかもしれません。

BIMを背景とした高速化かつ広域なデザイン発散とシミュレーションの後に，極めて古典的な（＝中身が分かり共有できる）統計処理を少し用いるだけで，「定量的な計画手法」という「言葉」が，意思決定の場で使える「道具」になっていることを共感して頂けたなら幸いです。

以上で投稿を終わります。

なお筆者が所属する立命館大学　建築都市デザイン学科では「BIM総合演習」としてまさにこのような流れを行う授業を行なっています。
「コンセプトモデルを立案し，統計的に優位なことを確認して，高く案をドライブさせよう！」という課題です。
Part 01 の冒頭にご紹介したプレゼンテーションがこの授業の提出物です。
変数は「デザイン性に関わる心理評価項目の自己評価」「同じ項目の他者評価」「日射熱取得量」「風速の分散」です。
最後にもう一度紹介して，この投稿を終えたいと思います。

下図の紙面右上はペアプロット図です。
この投稿に該当する内容はありませんが，自己評価と他者評価の傾向は相関関係にあるのか，デザイン性と日射熱取得量（環境美？）はどうか，等が読み取れる図です。個人的にはこちらも面白と思っています。
なおこの授業，BIMモデリングソフトの操作を丁寧に教える授業ではなく，よく言えば少し未来を見ている，でも何の役にも立たないかもしれない授業なので，あまり評判がよろしく無い気配，，，興味を持って貰うにはどうしたらよいのか，，，

お忙しい業務のなか，最後まで読んでくださった方，ありがとうございました。何かのお役に立てば幸いですm(_ _)m

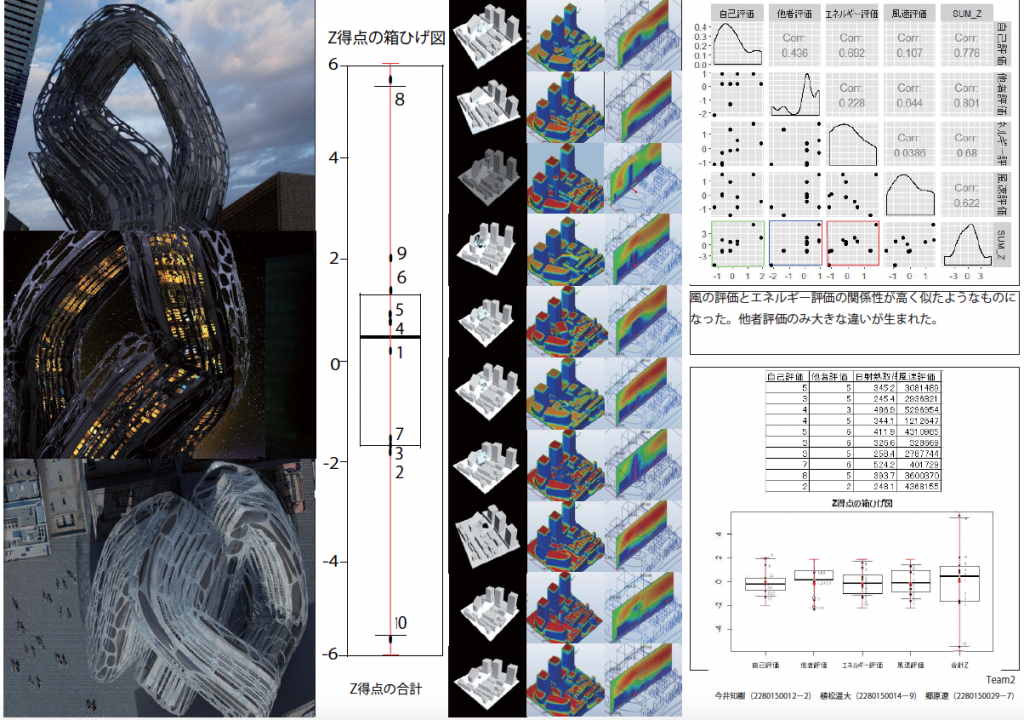
提出物（ドライブし過ぎ？（笑））